The Alderson disk

A homogeneous, thin, massive disk of outer radius R and inner radius a R (where 0 ≤ a < 1). G is the gravitational constant, M refers to the total mass of the (a = 0) disk (even in cases where a is nonzero). To zeroth order, the gravity "on" the disk can be approximated by that of an infinite plate (i.e. as being constant and directed vertical). The finite size of the disk causes noticeable deviations, in particular towards the inner and outer rim. These can be reduced by having the disk rotate around its axis of symmetry by a suitably chosen angular frequency Ω. In these examples, Ω is chosen such that the disk's outer and inner radius are on the same potential.

Structure of the gravitational field

The upper row (labelled "static") shows the situation due to gravity (disk + star) alone.
In the middle row, the disk is rigidly rotating with an angular velocity Ω, which is given in units of (GM/R³)^1/2.
The lower row depicts the field of a non-homogeneous disk whose area mass density varies according to the height of the white blocks. In other words, the blocky contour gives the variation in disk thickness in the case where the the mass density is constant, and the area density is solely determined by the disk's thickness. (Aspect ratio not to scale.)

1. Equipotentials

Shown are contours of constant total potential. The difference between adjacent contour lines is 5 % of the normalisation potential GM/R (10% in cases where a star is present). For clarity, contour lines close to the star are not shown. Numbers below the figures give the value of total potential at inner edge, center, and outer edge. (Click images to enlarge.)

2. Effective 'gravitational' acceleration within the disk

The lower set of images shows the variation of the radial (g_r, purple) and horizontal (g_z, red) component of the local acceleration, along with the absolute vector magnitude of g (green, dashed) in units of GM/R².

	a = 0 (no central hole)	a = 0.5, no star	a = 0.5, with (M/2) star
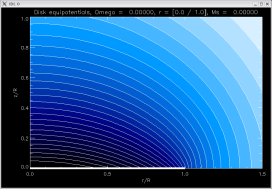
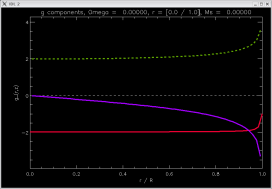
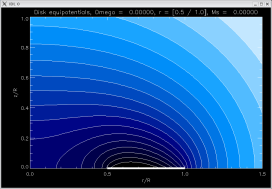
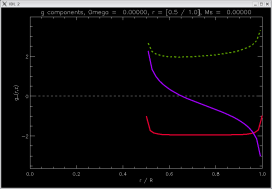
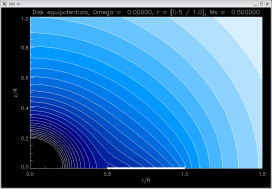
static	[ -2.0000, -1.86843, -1.27323 ]	[ -1.23181, -1.32279, -1.0145 ]	[ -2.23181, -1.98946, -1.5145 ]
-
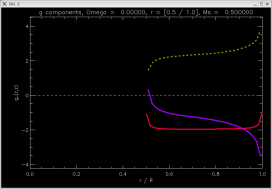
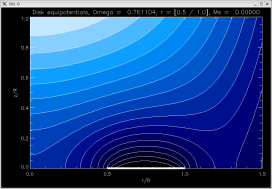
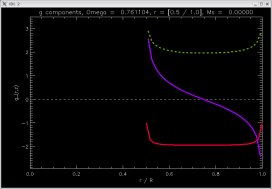
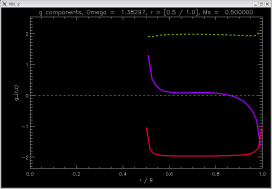
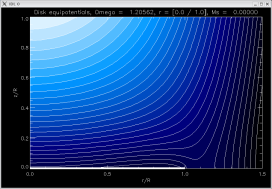
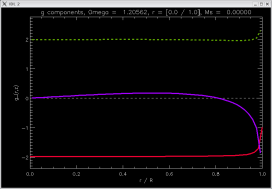
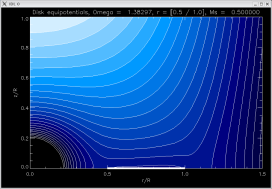
rotating	[ -2.0000, -2.05012, -2.0000 ]	[-1.30422, -1.48571, -1.30422 ]	[ -2.47088, -2.52738, -2.47088 ]
-
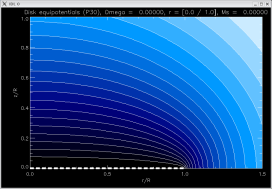
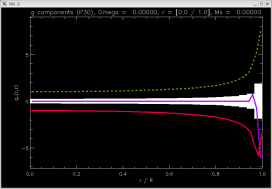
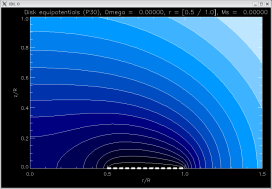
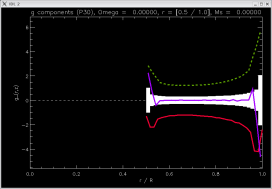
radially piecewise constant	[-1.57997, -1.57998, -1.48009]	[-1.15896, -1.24314, -1.06472 ]	Cannot have constant potential over the entire disk in the presence of a central point mass (or any other mass inside the ring, for that matter).
-
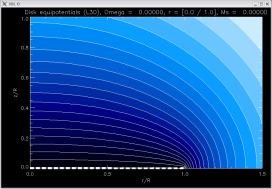
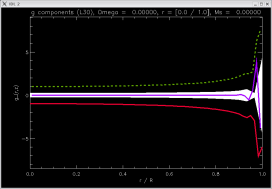
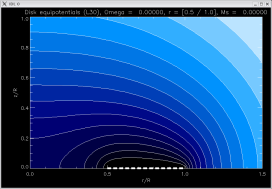
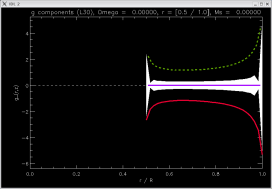
radially piecewise linear	[-1.56053, -1.56053, -1.56053]	[-1.19618, -1.19618, -1.19618]	Same as above...

How it's been done:

On a grid of 90x60 points in the desired rectangular area of r and z values, the respective values Φ_i,j for the gravitational potential are found by numerical computation of the corresponding integral using MuPAD. Since MuPAD seems to have difficulties doing contour plots for discrete data points (even if a smooth 2D spline is used for interpolation), the data are written to a file, then read into IDL. The potentials due to the central star's gravity Φ_star= -GM_star/(r²+z²)^1/2 and rotation Φ_rot = (Ω r)²/2 can easily be added due to superposition. For derivation of the Ω values see the above PDF.
For the inhomogeneous disk, the latter is partitioned into 30 annuli of equal thickness, where each of them is allowed to have a different area density μ_i. The potential field of each individual annulus is computed, and the μ's are fixed such that the potential on the central radius of each annulus is constant. The mathematical details are summarized in gravpot-disk.pdf.
The force of gravity at the disk level (z=0 with index j=0) is just the negative gradient of the potential, i.e. can be approximated using (g_r)_i+1/2,0 = - [Φ_i+1,0 - Φ_i,0] / [r_i+1,0 - r_i,0]
(g_z)_i,1/2 = - [Φ_i,1 - Φ_i,0] / [z_i,1 - z_i,0] .

Acknowledgements

Thanks to Tim Little and Erik Max Francis for raising several interesting points about this topic in the rec.arts.sf.science newsgroup.

Want to comment on this? Then go here.